Unitary FT

Demonstrate new argument to ft and ift that allows you to take an FT that’s unitary in the vector sense – this way, you don’t have to e.g. multiply by dt and divide by the number of points. (This is a standard capability with raw numpy, but we just had not much use for it before)

from pylab import *
from pyspecdata import *

fig, (ax_time, ax_freq) = subplots(2, 1)
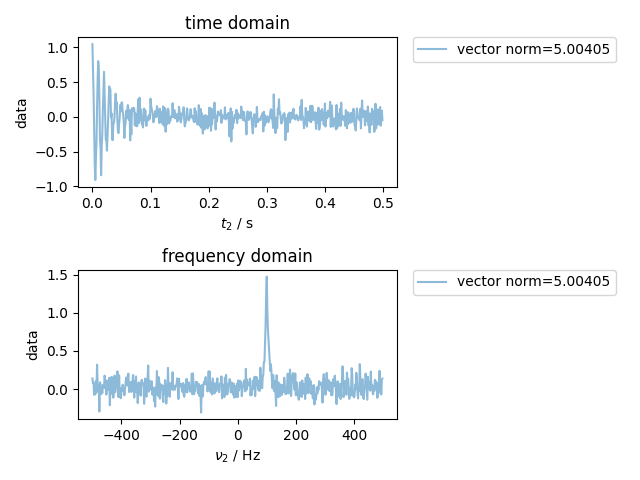
t = nddata(r_[0:0.5:1e-3], "t2")  # 1 kHz SW with a freq. resolution of 1/0.5=2 Hz
fake_data = exp(1j * 2 * pi * 100 * t - 10 * t * pi)  # 10 Hz wide line at 100 Hz offset
fake_data.add_noise(0.1).set_units("t2", "s")
logger.info(strm("vector norm of fake data, before ft", linalg.norm(fake_data.data)))
plot(
    fake_data,
    ax=ax_time,
    alpha=0.5,
    label="vector norm=%g" % linalg.norm(fake_data.data),
)
ax_time.set_title("time domain")
ax_freq.set_title("frequency domain")
fake_data.ft("t2", shift=True, unitary=True)
logger.info(
    strm("vector norm of fake data, after unitary ft", linalg.norm(fake_data.data))
)
assert fake_data.get_ft_prop("t2", "dt") == 1e-3
plot(
    fake_data,
    ax=ax_freq,
    alpha=0.5,
    label="vector norm=%g" % linalg.norm(fake_data.data),
)
fake_data.ift(
    "t2"
)  # because we already used "unitary" for the ft, it knows the ift is unitary.
#    In fact, passing "unitary" as a keyword argument will generate an error here
logger.info(
    strm("vector norm of fake data, after unitary ift", linalg.norm(fake_data.data))
)
ax_time.legend(**dict(bbox_to_anchor=(1.05, 1), loc=2, borderaxespad=0.0))
ax_freq.legend(**dict(bbox_to_anchor=(1.05, 1), loc=2, borderaxespad=0.0))
fig.tight_layout()
show()