1D BRD regularization

for 1D BRD, adapted mainly from Venkataramanan 2002 but checked against BRD 1981

• 
• 

----------  logging output to /home/jmfranck/pyspecdata.0.log  ----------
[(25, 'vd'), (100, '$\\log(T_1)$')]
[(100, '$\\log(T_1)$')]
[(25, 'vd')]
*** *** ***
[(25, 'vd')]
[(100, '$\\log(T_1)$')]
*** *** ***
[(100, '$\\log(T_1)$'), (25, 'lambda')]
[(25, 'vd'), (100, '$\\log(T_1)$')]
true mean: 0.009913670646611411 ± 0.09012035525083333
opt. λ mean: 0.017591517362925836 ± 0.03847965952228089
BRD mean: 0.011535665353561729 ± 0.01913456932196138

from pylab import *
from pyspecdata import *
from scipy.optimize import nnls
from numpy.random import seed
seed(1234)
init_logging('debug')
vd_list = nddata(linspace(5e-4,10,25),'vd')
t1_name = r'$\log(T_1)$'
logT1 = nddata(r_[-4:2:100j],t1_name)
def Gaussian_1d(axis,mu1,sigma1):
    this_G = exp(-(axis-mu1)**2/2/sigma1**2)
    return this_G
true_F = Gaussian_1d(logT1.C.run(lambda x: 10**(x)),6,0.3)


K = (1.-2*exp(-vd_list/10**(logT1)))

K.reorder('vd') # make sure vd along rows
print(shape(K))
print(shape(true_F))

M = K @ true_F # the fake data
print(shape(M))
#M.setaxis('vd',y_axis)
M.add_noise(0.2)

# this is here to test the integrated 1D-BRD (for pyspecdata)
print("*** *** ***")
print(ndshape(M))
print(ndshape(logT1))
print("*** *** ***")
solution = M.C.nnls('vd',logT1, lambda x,y: 1-2*exp(-x/10**(y)), l='BRD')

def nnls_reg(K,b,val):
    b_prime = r_[b,zeros(K.shape[1])]
    x,_ = nnls(A_prime(K,val),b_prime)
    return x

# generate the A matrix, which should have form of the original kernel
# and then an additional length corresponding to size of the data dimension, where smothing param val is placed
def A_prime(K,val):
    dimension = K.shape[1]
    A_prime = r_[K,val*eye(dimension)]
    return A_prime

plot_Lcurve = True
#{{{ L-curve
l = sqrt(logspace(-10,1,25)) # adjusting the left number will adjust the right side of L-curve

def vec_lcurve(l):
    return M.real.C.nnls('vd',
            logT1,lambda x,y: (1.-2*exp(-x/10**(y))), l=l)

# solution matrix for l different lambda values
x = vec_lcurve(l)
print(ndshape(x))
# norm of the residual (data - soln)
r_norm = x.get_prop('nnls_residual').data
# norm of the solution (taken along the fit axis)
x_norm = x.C.run(linalg.norm,t1_name).data

# From L-curve
this_L = 0.226

if plot_Lcurve:
    # Next plot the L-curve
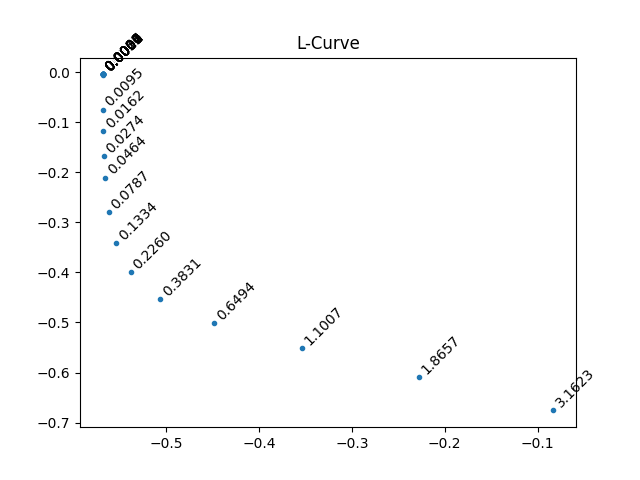
    figure();title('L-Curve')
    # I do not actually know why we take the log, but this is important for the shape
    plot(log10(r_norm[:]),log10(x_norm[:]),'.')
    annotate_plot = True
    show_lambda = True
    if annotate_plot:
        if show_lambda:
            for j,this_l in enumerate(l):
                annotate('%0.4f'%this_l, (log10(r_norm[j]),log10(x_norm[j])),
                         ha='left',va='bottom',rotation=45)
        else:
            for j,this_l in enumerate(l):
                annotate('%d'%j, (log10(r_norm[j]),log10(x_norm[j])),
                         ha='left',va='bottom',rotation=45)
#}}}

# generate data vector for smoothing

print(K.shape)
L_opt_vec = nnls_reg(K.data,M.data.squeeze(),this_L)

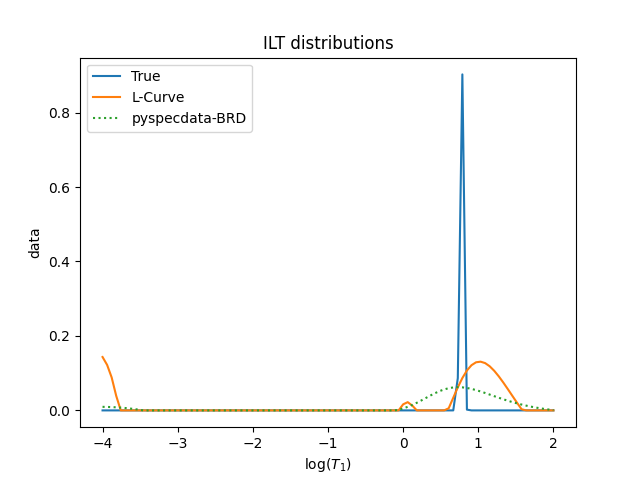
figure();title('ILT distributions')
L_opt_vec = nddata(L_opt_vec,t1_name).copy_axes(true_F)
plot(true_F,label='True')
print("true mean:",true_F.C.mean(t1_name).item(),"±",true_F.run(std,t1_name).item())
plot(L_opt_vec,label='L-Curve')
print("opt. λ mean:",L_opt_vec.C.mean(t1_name).item(),"±",L_opt_vec.run(std,t1_name).item())
plot(solution,':',label='pyspecdata-BRD')
print("BRD mean:",solution.C.mean(t1_name).item(),"±",solution.run(std,t1_name).item())
legend()
show()