Fit complex data with transform

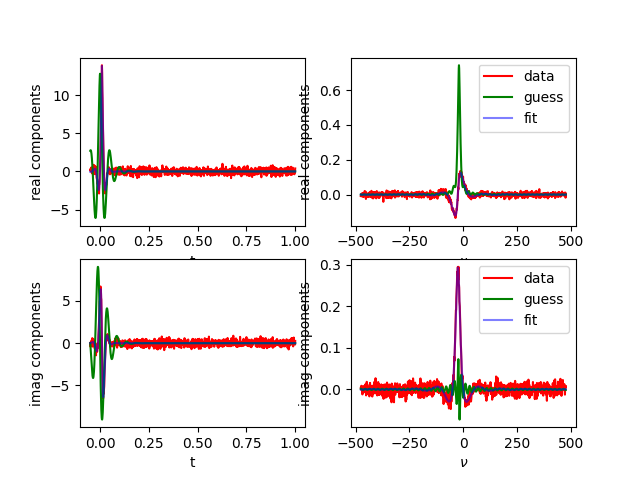
Using lmfitdata, fit a complex data set.

Use a transform to allow us to fit a peak in the frequency domain while leaving the definition of the peak in the time domain.

Why is this useful? Remember that for noiseless spectra, the norm of the residual might not be the same, but when we consider noisy spectra, it’s better to use the domain where the peak rises clearly above the noise. Also, in the “transform” we can do other things, such as masking, etc.

----------  logging output to /home/jmfranck/pyspecdata.0.log  ----------
--> fit_complex_with_transform.py(46):pyspecdata.core             <module> 2024-10-13 21:55:41,917
INFO: Functional Form: A*exp(-6.28318530717959*I*nu*(t - t_origin))*exp(-pi*R*Abs(t - t_origin))

import matplotlib.pyplot as plt
from numpy import pi
import sympy as sp
import numpy as np
from numpy import r_
import pyspecdata as psd

# initialize logging and set a seed so this runs the same every time
psd.init_logging(level="debug")
np.random.seed(15816)
A, R, nu, t, t_origin = sp.symbols("A R nu t t_origin", real=True)
# {{{ create an empty dataset and drop the fake data into it
thisfit = psd.lmfitdata(psd.nddata(r_[-0.05:1:1001j], "t"))


def my_residual_transform(d):
    d.ft("t")
    return d


thisfit.residual_transform = my_residual_transform
thisfit.functional_form = (
    A
    * sp.exp(-1j * 2 * pi * nu * (t - t_origin))
    * sp.exp(-R * sp.pi * abs(t - t_origin))
)
psd.logger.info(psd.strm("Functional Form:", thisfit.functional_form))
# {{{ if you set only_real to True, it previously worked -- this
#     example demonstrates that this also works when set to False
only_real = False
if only_real:
    thisfit.functional_form = sp.re(thisfit.functional_form)
# }}}
# {{{ create the "true" parameters for the fake data by pretending like
#     the true values are a guess, and then outputting the guess data
true_values = {"A": 14.0, "R": 30, "nu": 25, "t_origin": 0.01}
thisfit.set_guess(true_values)
# {{{ here, just set the ft startpoints -- as noted
#     elsewhere, we should have a function to do this
#     without actually doing the transform
thisfit.ft("t", shift=True).ift("t")
# }}}
# }}}
mydata = thisfit.settoguess().eval()
mydata.add_noise(0.01)
fig, ((ax3, ax1), (ax4, ax2)) = plt.subplots(2, 2)
psd.plot(mydata, "r", label="data", ax=ax1)
psd.plot(mydata.imag, "r", label="data", ax=ax2)
mydata.ift("t")
psd.plot(mydata, "r", label="data", ax=ax3)
psd.plot(mydata.imag, "r", label="data", ax=ax4)
# }}}
# {{{ set up the fit object using the "simulated" data
#     here we need to IFT above, since "eval" above
#     generates in the frequency domain
newfit = psd.lmfitdata(mydata.C)
newfit.functional_form = thisfit.functional_form
newfit.set_guess(
    A=dict(value=13.0, max=20, min=0.0),
    R=dict(value=10, max=1000, min=0),
    nu=dict(value=20),
    t_origin=dict(value=0.0, min=-0.1, max=0.1),
)
newfit.residual_transform = my_residual_transform
# }}}
# {{{ show the guess
guess = newfit.settoguess().eval()
psd.plot(guess, "g--", label="guess", ax=ax1)
psd.plot(guess.imag, "g--", label="guess", ax=ax2)
guess.ift("t")
psd.plot(guess, "g--", label="guess", ax=ax3)
psd.plot(guess.imag, "g--", label="guess", ax=ax4)
# }}}
# {{{ run the fit and generate nddata
newfit.fit()
plotdata = newfit.eval()
psd.plot(plotdata, "b", alpha=0.5, label="fit", ax=ax1)
psd.plot(plotdata.imag, "b", alpha=0.5, label="fit", ax=ax2)
plotdata.ift("t")
psd.plot(plotdata, "b", alpha=0.5, label="fit", ax=ax3)
psd.plot(plotdata.imag, "b", alpha=0.5, label="fit", ax=ax4)
# }}}
ax1.set_ylabel("real components")
ax2.set_ylabel("imag components")
ax3.set_ylabel("real components")
ax4.set_ylabel("imag components")
ax1.legend()
ax2.legend()
plt.show()